PHP Random Number Generator with Normal Distribution / Bell Curve
So for a project we needed some random test data but we wanted the data to be on a bell curve to represent real life scenarios. I couldn’t find anything so after so digging I found some code in Java and translated it into php seems to work great.
function purebell($min,$max,$std_deviation,$step=1) {
$rand1 = (float)mt_rand()/(float)mt_getrandmax();
$rand2 = (float)mt_rand()/(float)mt_getrandmax();
$gaussian_number = sqrt(-2 * log($rand1)) * cos(2 * M_PI * $rand2);
$mean = ($max + $min) / 2;
$random_number = ($gaussian_number * $std_deviation) + $mean;
$random_number = round($random_number / $step) * $step;
if($random_number < $min || $random_number > $max) {
$random_number = purebell($min, $max,$std_deviation);
}
return $random_number;
}
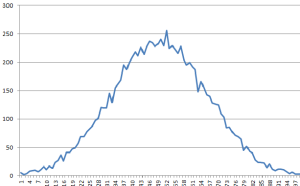
When I ran through it 10,000 times with a min of 1 and a max of 100 and a standard deviation of 3 here is the distribution I got, I would say that looks like a bell curve.
Update and credit to Stefan Muth for his comment below. He has made some tweaks and even added some functionality to allow you to skew results and change the standard deviation. Here is the code he created:
// Generate a random integer between $min and $max on a bell curve
function intBell($min, $max, $mid=0.5, $std_deviation=1) {
if ($min == $max) return $max;
$n = floatBell($min, $max, $mid, $std_deviation);
return floor((($n - $min) * ($max - $min + 1) / ($max - $min)) + $min);
}
// Generate a random float between $min and $max on a bell curve
// - Increasing $std_deviation flattens it
// - Increasing $mid skews it to the right
function floatBell($min, $max, $mid=0.5, $std_deviation=1) {
if ($min == $max) return $max;
$d = (float)mt_getrandmax();
$r1 = (float)mt_rand() / $d;
$r2 = (float)mt_rand() / $d;
$gaussian_number = sqrt(-2 * log($r1)) * cos(2 * M_PI * $r2);
$mean = ($max + $min) * $mid;
$random_number = ($gaussian_number * $std_deviation) + $mean;
if($random_number < $min || $random_number > $max) {
$random_number = floatBell($min, $max, $mid, $std_deviation);
}
return $random_number;
}
Thanks for this it will be very helpful in creating test data.
Hi, thanks for the code, it seems to do exactly what I need ! 🙂
But I’m still having trouble understanding how you got that graph … Could you tell me if it needs a loop or anything ?
Thanks man ! 🙂
Glad it was helpful.
Yes I ran a loop that ran this function 10,000 times then just took the numbers generated and put them into Excel to generate the graph. You could generate the graph with a PHP library if you wanted.
Hi Nate,
I think there is a serious flaw in your formula. Either that or I’ve screwed up really badly. I tried using the function but I kept getting skewed results. I tried it for min = 5, max = 15, sd = 3.5. I kept getting the values skewed as if 9.5 was the high point, not 10. It also seemed to be “cut” from the right.
Here are the results of a sample run with 500 000 generated numbers, split in buckets of 0.5 (5.0-5.5, 5.5-6.0, 6.0-6.5, etc.):
1368
2949
6069
11089
18161
27440
37074
45403
49994
49897
45445
36969
27585
18321
11070
6116
2986
1332
514
218
You don’t even need a graph to see the problem.
After modifying those two rows like so:
$half = ($max – $min) / 2;
$middle = $min + $half;
I was able to produce numbers in a good distribution:
238
666
1814
4307
8888
16415
26487
38290
48544
54627
54577
48427
37939
26517
16594
8787
4107
1837
688
251
I failed to understand why those two rows that calculate the half and the middle are the way you made them but fixing them like I describe seems to have fixed my problem. Please, let me know if I missed something important they are supposed to do in the way you’ve written them.
Best,
Georgi
Yeah it believe it has to do with whether you have an even or odd number of possible results. For example in your case 5 to 15 = 11 possible results, 1 to 100 = 100 possible results. I’ll update the function so that it checks for that. Thanks for the feedback.
I’m glad I helped, but I’m not sure I get your reasoning for even and odd numbers.
$half = ($max – $min + 1) / 2;
$middle = $min + $half – 1;
With values of 1 and 100 it would produce $half = 50 when it should be 49.5 (100 = 1 + 49.5 + 49.5) and $middle = 49.5 when it should be 50.5.
Nope that wasn’t it either I just updated again. I just used the mean and round() (instead of intval) now and it is working great.
I also just added a new input variable for the step so you can send in $step = .5 and it will give you back the numbers rounded off to the closest .5 value (defaults to $step = 1).
I did a trial run of the function with 0.5 for $step and it generated only integers.
I think this line does nothing:
$random_number = round($random_number / $step) * $step;
$random_number = 8 =>
round(8 / 0.5) * 0.5 = round (16) * 0.5 = 16 * 0.5 = 8…
It works if you are storing them in an array make sure you use quotes around the key (I had that issue the first time i tried.) I did it and got the following results:
Array
(
[5] => 170
[5.5] => 210
[6] => 303
[6.5] => 358
[7] => 492
[7.5] => 464
[8] => 607
[8.5] => 601
[9] => 695
[9.5] => 654
[10] => 821
[10.5] => 688
[11] => 759
[11.5] => 617
[12] => 588
[12.5] => 447
[13] => 480
[13.5] => 328
[14] => 304
[14.5] => 219
[15] => 195
)
Before this line:
$random_number = round($random_number / $step) * $step;
$random_number is a float so it would look something like this 8.35 (lot more decimal places though) then when you divide by .5 you would get 16.7 which would round up to 17. Then 17 * .5 = 8.5.
Well, I’ve run the function and it doesn’t generate anything different than integers.
$random_number is always an integer, since you have:
$random_number = round(($gaussian_number * $std_deviation) + $mean);
just before
$random_number = round($random_number / $step) * $step;
So I would submit that any integer divided by 0.5 (multiplied by 2) will always result in an even integer. And then dividing that integer by 2… the line is pointless unless you remove the “round” function from the previous line.
Your correct, sorry it was a copy and paste error forgot to remove the round() on the line before. Sorry for the confusion.
Forgot to mention – you might want to use mt_rand() & mt_getrandmax() instead of rand() and getrandmax().
Yes if you want better random numbers then yes I would use those functions. However, they are much slower functions so I guess it all depends on whether you are looking for speed or precision.
I’ve actually read on several places that mt_rand uses a better algo and is up to 4x faster than rand. Turns out this is information is outdated, but I would not agree that it is slower than rand(). Running a few tests with 10 million iterations showed both functions exhibiting the exact same speed ~4 seconds on my VPS.
Your right I did some more digging and according to PHP documentation mt_rand() is faster. I went ahead and updated it to use the mt_ functions. Thanks again.
Thankyou!
As being said, this is a great tool for creating test data!
Hi, can you post a sample of the code you used to generate the graph? I would like to test it on my server.
I just used Excel to generate the graph, no code.
Great work, thanks for sharing 🙂
Wtf ? It should not be a Bell curve. It should be straight horizontal curve.
Pls @Pitchinnate and @Georgi update the code because this one here isn’t generating a bell shaped curve when the code is executed
Sorry I haven’t looked at this in a long time. I just tested and it seems to still work without any issues for me. What issue are you having?
Thanks to your post, you have given me the only practical solution to this problem that I could find after hours of searching, so THANK YOU!
However, there is a problem with this function when it comes to generating random *integers* (as array indices for example) as others have noticed:
Say you want to generate random integers between 1 and 7 on a bell curve.
Your function will correctly give you FLOAT values ranging from 1.000… to 6.999…
HOWEVER, for getting INTEGER values 1 to 7, this will not work because int(1.000…) = 1 but int(6.999…) = 6.
Changing “$max” to “$max + 1” inside the function will lead to compound errors due to the recursion.
Here is how to convert a float $n in the range $min to $max into an integer ranging from $min to $max:
floor((($n – $min) * $max / ($max – 1)) + $min)
I have modified your function to include a $mid value to allow for easy skewing, and turned it into two functions that generate either a random bell-curve integer or float as required. I also removed the $step parameter because this is easily handled outside the function. Feel free to take anything from it that you like… it works perfectly as-is though:
// Generate a random integer between $min and $max on a bell curve
function intbell($min, $max, $mid=0.5, $std_deviation=1) {
$n = floatbell($min, $max, $mid, $std_deviation);
return floor((($n – $min) * $max / ($max – 1)) + $min);
}
// Generate a random float between $min and $max on a bell curve
// – Increasing $std_deviation flattens it
// – Increasing $mid skews it to the right
function floatbell($min, $max, $mid=0.5, $std_deviation=1) {
$d = (float)mt_getrandmax();
$r1 = (float)mt_rand() / $d;
$r2 = (float)mt_rand() / $d;
$gaussian_number = sqrt(-2 * log($r1)) * cos(2 * M_PI * $r2);
$mean = ($max + $min) * $mid;
$random_number = ($gaussian_number * $std_deviation) + $mean;
if($random_number $max) {
$random_number = floatbell($min, $max, $mid, $std_deviation);
}
return $random_number;
* Regarding the above post, the trailing “}” is missing and, because of the ‘less than’ sign being interpreted (stripped) as an HTML tag in this comments section, some of the code is missing in the recursion test line. I am happy to provide the full code to anyone who emails me at diagnose (aat) gmail (doot) com.
Apologies for a third post (perhaps Nate can edit/combine them):
Upon further testing, the formula
floor((($n – $min) * $max / ($max – 1)) + $min)
… only works in the specific case when $min = 1.
The correct code that works for any range of integers is:
floor((($n – $min) * ($max – $min + 1) / ($max – $min)) + $min);
Good catch I will review and update the post.